01) 문제
KOI 사냥터에는 N 마리의 동물들이 각각 특정한 위치에 살고 있다. 사냥터에 온 사냥꾼은 일직선 상에 위치한 M 개의 사대(총을 쏘는 장소)에서만 사격이 가능하다. 편의상, 일직선을 x-축이라 가정하고, 사대의 위치 x1, x2, ..., xM은 x-좌표 값이라고 하자. 각 동물이 사는 위치는 (a1, b1), (a2, b2), ..., (aN, bN)과 같이 x,y-좌표 값으로 표시하자. 동물의 위치를 나타내는 모든 좌표 값은 양의 정수이다.
사냥꾼이 가지고 있는 총의 사정거리가 L이라고 하면, 사냥꾼은 한 사대에서 거리가 L 보다 작거나 같은 위치의 동물들을 잡을 수 있다고 한다. 단, 사대의 위치 xi와 동물의 위치 (aj, bj) 간의 거리는 |xi-aj| + bj로 계산한다.
예를 들어, 아래의 그림과 같은 사냥터를 생각해 보자. (사대는 작은 사각형으로, 동물의 위치는 작은 원으로 표시되어 있다.) 사정거리 L이 4라고 하면, 점선으로 표시된 영역은 왼쪽에서 세 번째 사대에서 사냥이 가능한 영역이다.
사대의 위치와 동물들의 위치가 주어졌을 때, 잡을 수 있는 동물의 수를 출력하는 프로그램을 작성하시오.
입/출력
입력의 첫 줄에는 사대의 수 M (1 ≤ M ≤ 100,000), 동물의 수 N (1 ≤ N ≤ 100,000), 사정거리 L (1 ≤ L ≤ 1,000,000,000)이 빈칸을 사이에 두고 주어진다. 두 번째 줄에는 사대의 위치를 나타내는 M개의 x-좌표 값이 빈칸을 사이에 두고 양의 정수로 주어진다. 이후 N개의 각 줄에는 각 동물의 사는 위치를 나타내는 좌표 값이 x-좌표 값, y-좌표 값의 순서로 빈칸을 사이에 두고 양의 정수로 주어진다. 사대의 위치가 겹치는 경우는 없으며, 동물들의 위치가 겹치는 경우도 없다. 모든 좌표 값은 1,000,000,000보다 작거나 같은 양의 정수이다.
출력은 단 한 줄이며, 잡을 수 있는 동물의 수를 음수가 아닌 정수로 출력한다.
4 8 4
6 1 4 9
7 2
3 3
4 5
5 1
2 2
1 4
8 4
9 4
# output is 6서브태스크
| 번호 | 배점 | 제한 |
|---|---|---|
| 1 | 9 | M ≤ 10, N ≤ 10, X ≤ 10 |
| 2 | 14 | M ≤ 20, N ≤ 20, X ≤ 20 |
| 3 | 18 | M ≤ 100, N ≤ 100 |
| 4 | 19 | M ≤ 2,000, N ≤ 2,000 |
| 5 | 40 | 추가적인 제약 조건은 없다. |
02) 풀이
각 사대에 대해 사정거리 안의 동물의 수를 각각 구한 다음 중복을 제거해주는 접근을 먼저 떠올렸는데, 중복 제거 과정의 구현방법이 잘 생각나지 않았다. 그래서 각 점의 입장에서 사대의 사정거리 안에 포함되는지의 여부를 체크한 다음, 어떤 한 사대의 사정거리에도 포함되지 않는다면 제외할 점으로 카운팅해주도록 했다.
M, N, L # 각각 사대의 개수, 동물(점)의 개수, 사정거리
m = list[int 0 .. M-1] # 사대의 좌표 배열
n = list[[x, y] 0 .. N-1] # 점의 좌표 배열
excp = 0 # 제외할 점의 개수
for i in range(N):
if 사정거리 안에 없음:
excp += 1
..사정거리 안에 없음을 판단할 수 있는 조건은 두 가지로 생각했다.
점 $\ a = (x_a,\space y_a)$ 과 사정거리 $\ L$ 에 대하여,
- 만약 점의 $\ y_a > L$ 이면 사정거리 안에 없다.
- $\ y_a \le L$일 때, $\ x_a$부터 양쪽으로 각각 $\ (L-y_a)$ 만큼 떨어진 거리 내에 사대가 존재하지 않는다면, 사정거리 안에 없다.
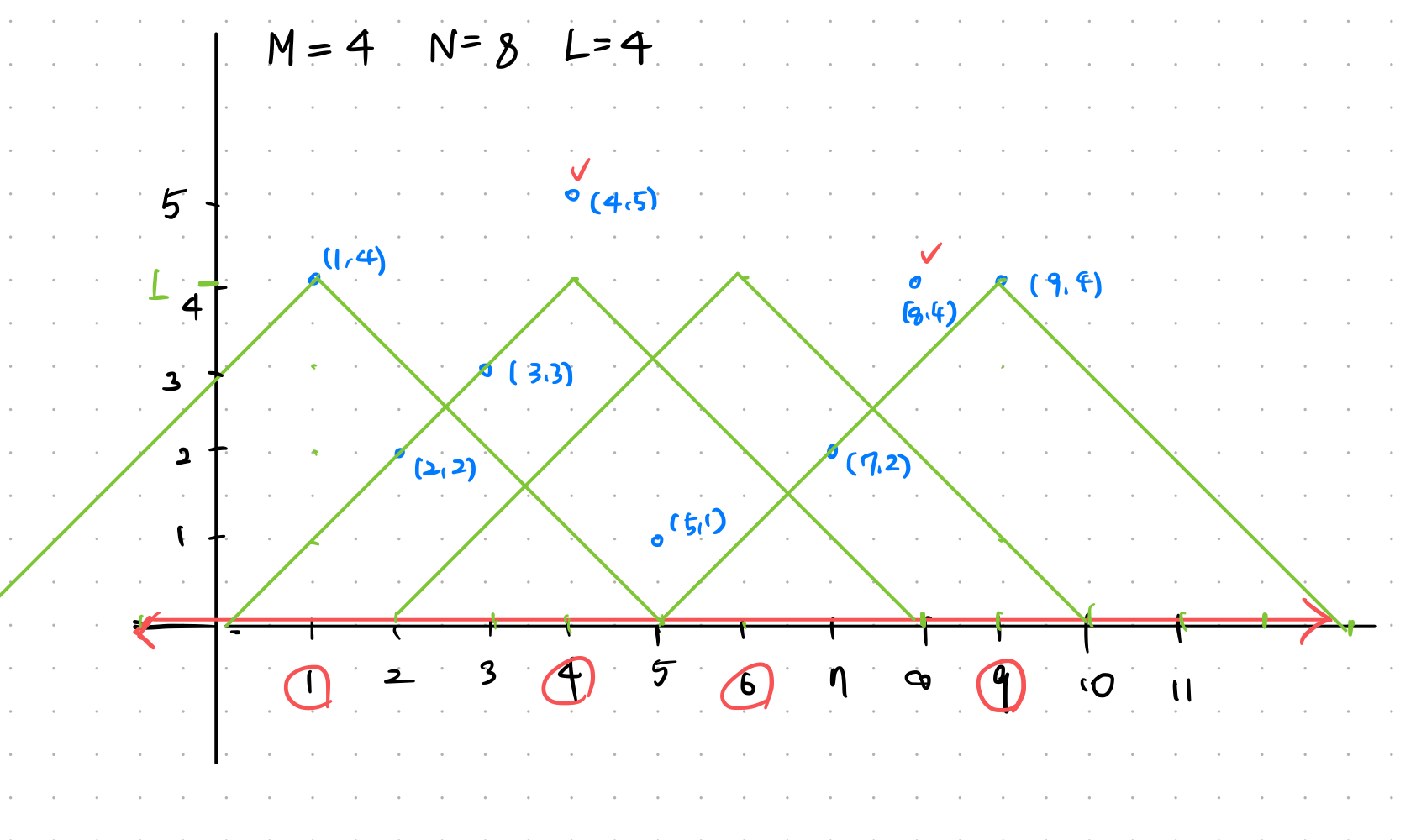
위와 같은 그림에서, 점 (4, 5)는 y좌표 5가 사정거리 L=4 보다 크기 때문에 벗어나는 것을 볼 수 있다.
또 점 (8, 4)도 사정거리를 벗어난다. 이는 $\ x = 8 $ 로부터 양쪽으로 $\ (L-y) = (4, 4) = 0 $ 만큼 떨어진 곳에 사대가 없기 때문이다. 즉 좌표 8에 사대가 없으므로, 사정거리를 벗어날 수 있다. 두 번째 조건을 구간으로 표현하면 아래와 같다.
$\ (s, e) = (x-(L-y), \space x+(L-y)) $

위 그림을 보면, y좌표가 L에 가까워질수록 사정거리에서 벗어나기 위한 x좌표와 사대와의 거리가 4, 3, 2, 1로 점차 줄어드는 것을 볼 수 있다.
따라서, y좌표가 L이하인 각 점에 대해서는, 사정거리에서 벗어나기 위한 구간 (s, e)를 계산하고, 이 구간 내 사대가 존재하는지만 체크하면 된다.
attackable() 함수의 구현
1. 첫 번째 방법: 단순 반복 O(L)
def attackable(x, y):
s, e = x-(L-y), x+(L-y)
for i in range(s, e+1):
if i in m:
return True
return False점의 x, y좌표를 파라미터로 받아, 구간 (s, e) 내 사대의 존재 여부를 체크하여 반환하는 attackable() 함수를 구현한다고 하자. 가장 간단하게는 위와 같이 이 구간의 모든 양의 정수에 대해 사대의 배열 m에 존재하는지를 체크하는 단순 반복문이 있을 수 있다. 이 함수를 사용할 경우, 점수는 40점이 나온다.
이유는 구간 (s, e)의 길이가 L에 의존하는데, 문제에서 주어진 L의 범위가 (1 <= L <= 1,000,000,000)이기 때문이다. 최대 2*L번 반복문을 수행하므로 당연히 실행 시간이 길어져 시간 초과가 발생한다.
2. 두 번째 방법: 이중 포인터 O(M)
def attackable():
s, e = x-(L-y), x+(L-y)
# 만약 s == e 이면 이 x좌표에 사대가 있는지만 검사
if s == e:
return s in m
i, j, k = 0, M-1, 0
# two pointer로 m[i] < s 이거나 m[i] > e 인 인덱스 검색
while k < M:
if m[i] < s:
i += 1
if m[j] > e:
j -= 1
if i >= j:
break
k += 1
if i > j:
return False
if i == j:
if i == s or i == e:
return False
# 만난 값이 (s, e)에 속하는지 반환
return s <= m[i] <= e
return True그래서 L의 크기에 의존하지 않는 방식으로 함수를 구현해보았다. m배열이 오름차순으로 정렬되어 있으므로, 양 끝에서부터 이중 포인터를 사용하여 존재 여부를 체크할 수 있다. 앞에서부터 시작하는 포인터 i는 m[i] < s 일때 1 증가하며 배열을 검사한다. 뒤에서부터 시작하는 포인터 j는 m[j] > e 일때 1 감소하며 배열을 검사한다. 만약 i >= j 라면 반복문을 탈출한다.
i == j 인 경우 이 인덱스의 사대가 구간 (s, e)에 포함되는지 한번 더 검사하고 결과를 반환한다. i > j인 경우 구간이 존재하지 않는다.
🥲 하나하나 값을 넣어가면서 디버깅하며 코드를 짰기에 코드가 지저분하다ㅜㅜ 이 이하로 케이스를 나누어 검사하는 방식도 있을 것 같다. 추후 개선해 볼 것. 이 코드를 사용할 경우 복잡도는 O(M)이다. 최대 M번 모든 사대를 검사할 수 있기 때문이다. 점수는 60점이 나왔다.
3. 세 번째 방법: 이진 탐색 O(logM)
def attackable():
s, e = x-(L-y), x+(L-y)
# 검사할 필요가 없는 경우
if m[-1] < s or m[0] > e:
return False
# 만약 s = e이면 이 점이 사대인지만 확인
if s == e:
return s in m
v1, v2 = 0, M-1
if m[0] >= s:
# 만약 첫번재 원소가 s보다 >=, 모든 원소가 s보다 >= (all T)
v1 = 0
else:
# m[i] >= s 인 최소의 값 v1 탐색: lower bound
# s보다 크거나 같은 수가 처음 등장하는 위치를 찾는다
low, high = 0, M-1
while low+1 < high: # low와 high 사이에는 한 칸 존재
mid = (low+high)//2
if m[mid] >= s: # if true
high = mid
else:
low = mid
v1 = high
if m[-1] <= e:
# 만약 마지막 원소가 e보다 <=, 모든 원소가 e보다 <= (all F)
v2 = M-1
else:
# m[i] > e 인 최소의 값 v2 탐색: upper bound
# e보다 큰 수가 처음 등장하는 위치를 찾는다
# 찾은 후 high-1 하면 e보다 작거나 같은 수의 최대 인덱스가 된다
low, high = 0, M-1
while low+1 < high:
mid = (low+high)//2
if m[mid] > e: # if true
high = mid
else:
low = mid
v2 = high-1
# 만약 v1 > v2라면 범위는 없다
if v1 > v2:
return False
return True복잡도를 logM으로 줄여 줄 수 있는 이진 탐색을 활용한 방법이다. 접근법은 이중 포인터와 유사하다. 먼저 m[i] >= s 인 최소의 i를 찾는다. 그리고 m[j] <= e인 최대의 j를 찾는다. 그리고 i 와 j의 위치를 비교하여 구간의 존재 여부를 체크한다.
이진/이분 탐색 Binary Search는 배열을 둘로 나누어 가면서 최적값을 찾기 때문에 위와 같은 상황에서 보다 적은 시간복잡도로 코드를 짤 수 있다. 아이디어는 이해가 갔지만, low, mid, high의 값을 잘못 설정하면 오답을 뱉기 때문에 구현에서 헷갈리는 부분이 많았다. (그리고 반복문 탈출의 조건을 정확히 넣어두지 않으면 무한루프로 돌아간다ㅜㅜ)
그 때 도움이 많이 되었던 글 로 인해 어느 정도 감을 잡은 것 같다. 주요 포인트는
- 배열이 모두 True 또는 모두 False가 되지 않도록 예외처리 먼저
- T to F 또는 F to T 배열에 대해 값이 달라지는 경계를 검색
- 만약 check(low) != mid 이면 high = mid
- 아니면 low = mid
- 마지막에는 low 바로 다음이 high가 된다.
- 이 때 구하고자 하는 답이 low인지 high인지 생각하여 최종 답을 낸다
이 포인트를 가지고 attackable() 함수의 진행 과정을 나타내면 다음과 같다.
# 구간 (s, e)에 배열 X의 값이 존재하면 True, 아니면 False
오름차순으로 정렬된 배열 X와 s <= e인 구간 (s, e)에 대해,
1. s == e 이면:
return s in X
2. X[i] >= s인 최소 i의 값 v1 찾기
a. if X[0] >= s 이면 모두 True인 배열이 된다.
따라서 v1 = 0
b. if X[-1] < s 이면 모두 False인 배열이 된다.
검사할 필요 없이, return False
c. if False to True 이면
경계를 이분 탐색한다.
while low+1 < high:
mid = (low+high)//2
if X[mid] >= s: # true 이면
high = mid
else:
low = mid
v1 = high # true인 값을 가져옴
3. X[j] <= e인 최대 j의 값 v2 찾기
먼저 X[j] > e인 최소 j를 찾고, v2 = j-1
a. if X[0] > e 이면 모두 True 인 배열이 된다.
검사할 필요 없이, return False
b. if X[-1] <= e 이면 모두 False 인 배열이 된다.
v2 = len(X)-1 마지막 원소
c. if False to True 이면
while low+1 < high:
mid = (low+high)//2
if X[mid] > e:
high = mid
else:
low = mid
# high는 e보다 큰 최소
# 따라서 high-1은 e보다 작거나 같은 최대
v2 = high - 1
4. if v1 > v2:
범위가 존재하지 않으므로 return False
5. else:
범위에 해당하는 하나 이상의 원소가 있음
return True복잡해 보이지만, 예시를 들어보면 간단하다.
X = [12, 14, 25, 37, 100, 105, 200]
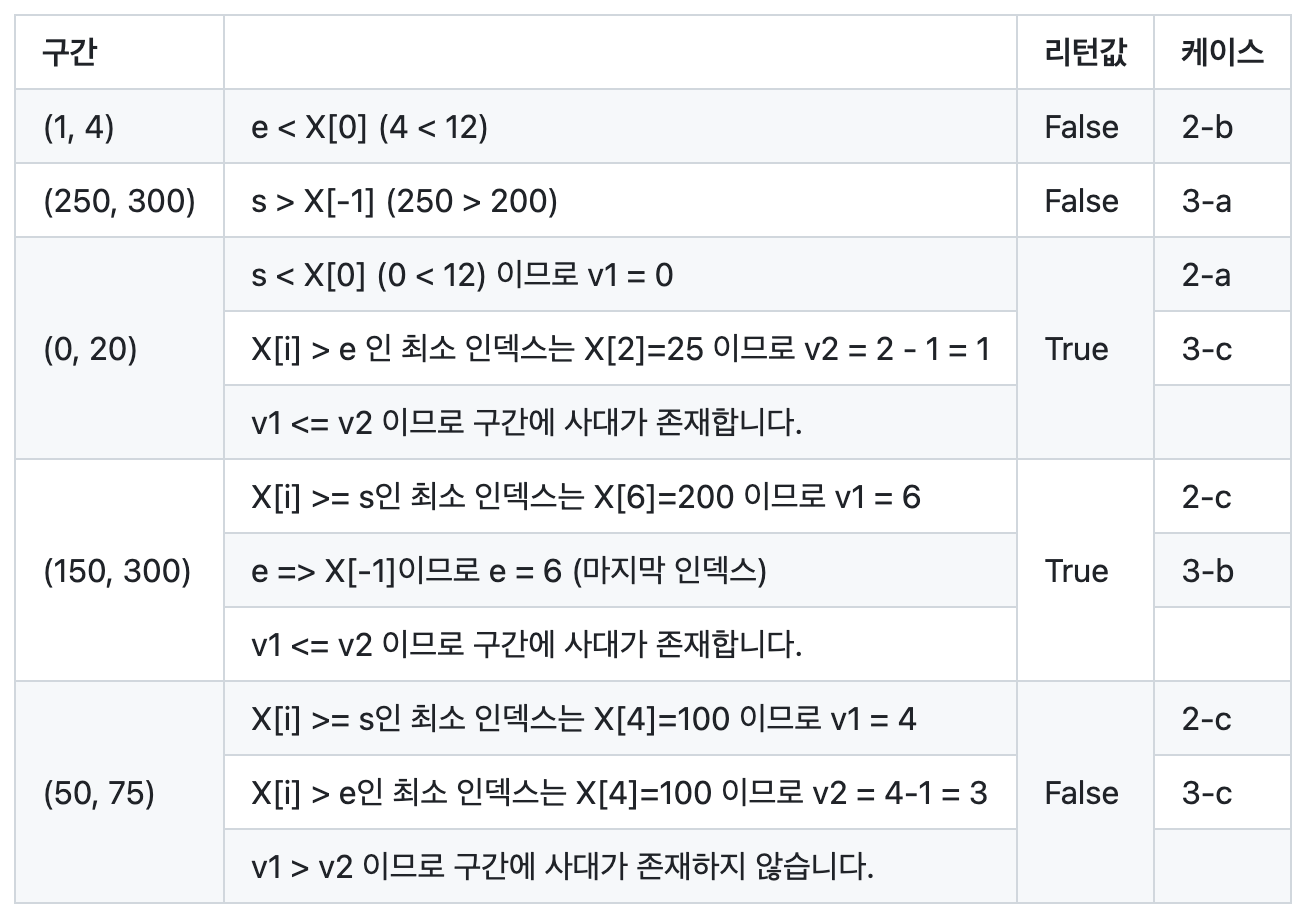
+) lower/upper bounds?
위에 사용한 것과 같이, 정렬된 배열에서 특정값 k 이상 또는 초과인 최솟값을 찾는 것을 lower bound, upper bound 함수라고 부른다. 나는 e보다 작거나 같은 최댓값을 찾기 위해 upper bound를 찾은 후 -1 해주었다.
- lower bound: X[i] >= k인 최소의 인덱스 i 찾기 (k이상인 값이 첫 번째로 등장하는 위치)
- upper bound: X[i] > k인 최소의 인덱스 i 찾기 (k보다 큰 값이 첫 번째로 등장하는 위치)
이진 탐색에서 실수가 없도록 문제를 꼼꼼히 읽고 가능한 모든 케이스들을 고려해야 한다.
어쨌든, 이대로 코드를 사용하면 100점을 받을 수 있다 !
03) 코드 (파이썬)
def attackable(x, y): # binary search
s, e = x-(L-y), x+(L-y)
# 검사할 필요가 없는 경우
if m[-1] < s or m[0] > e:
return False
# 만약 s = e이면 이 점이 사대인지만 확인
if s == e:
return s in m
v1, v2 = 0, M-1
if m[0] >= s:
# 만약 첫번재 원소가 s보다 >=, 모든 원소가 s보다 >= (all T)
v1 = 0
else:
# m[i] >= s 인 최소의 값 v1 탐색: lower bound
# s보다 크거나 같은 수가 처음 등장하는 위치를 찾는다
low, high = 0, M-1
while low+1 < high:
mid = (low+high)//2
if m[mid] >= s: # if true
high = mid
else:
low = mid
v1 = high
if m[-1] <= e:
# 만약 마지막 원소가 e보다 <=, 모든 원소가 e보다 <= (all F)
v2 = M-1
else:
# m[i] > e 인 최소의 값 v2 탐색: upper bound
# e보다 큰 수가 처음 등장하는 위치를 찾는다
# 찾은 후 high-1 하면 e보다 작거나 같은 수의 최대 인덱스가 된다
low, high = 0, M-1
while low+1 < high:
mid = (low+high)//2
if m[mid] > e: # if true
high = mid
else:
low = mid
v2 = high-1
# 만약 v1 > v2라면 범위는 없다
if v1 > v2:
return False
return True
M, N, L = map(int, input().split())
m = list(map(int, input().split()))
n = [list(map(int, sys.stdin.readline().split())) for _ in range(N)]
m.sort()
lower = m[0]-L
upper = m[-1]-L
excp = 0
# y좌표가 L을 초과하면 제외하고
# 모든 점에 대해 사정거리 안에 있는지 여부 조사
for i in range(N):
if n[i][1] > L:
excp += 1
continue
if not attackable(n[i][0], n[i][1]):
excp += 1
print(N-excp)이진 탐색 문제를 처음 접했을 때는 무슨 말인지 하나도 이해 못하고 풀이를 봐도 모르겠어서 그저 울고만 싶었는데, 그래도 하나둘씩 찾아보면서 어느 정도 (약 1%) 감을 잡은 것 같다. 이 문제도 나름 골드4인데.. 이진 탐색 구현을 잘 못 해서 방법을 검색해보긴 했지만, 답안 없이 스스로 접근법까지는 생각해낼 수 있었다는 것이 뿌듯하다 :) 다음에는 실수 없이 구현까지 능숙하게 마무리할 수 있도록 많이 연습하자👊
Reference
이분 탐색(Binary Search) 헷갈리지 않게 구현하기
Theme 03. STL 알고리즘 _ lower_bound, upper_bound
'DevLog 📨 > Baekjoon' 카테고리의 다른 글
| [DevLog][Baekjoon] 1655: 가운데를 말해요 (0) | 2023.08.20 |
|---|---|
| [DevLog][Baekjoon] 2110: 공유기 설치 (0) | 2023.08.16 |
| [DevLog][Baekjoon] 2261: 가장 가까운 두 점 (0) | 2023.08.14 |
| [DevLog][Baekjoon] 1629: 곱셈 (0) | 2023.08.14 |
| [BaekJoon] 1007: 벡터 매칭 (0) | 2023.02.16 |